Binary Search

Binary search algorithm for efficiently finding elements in sorted arrays and search spaces

Medium Algorithm Basic binary search Search in rotated array Find boundaries Search in 2D matrix Optimization problems

Binary Search

Overview

Binary Search is an efficient algorithm to find a target value in a sorted search space using two pointers.

Key Properties

Time Complexity: O(log n)
Space Complexity: O(1) iterative, O(log n) recursive
Prerequisites: Sorted array OR monotonic property
Search Space: Not limited to fully sorted arrays - works with:
- Fully sorted arrays
- Partially sorted arrays
- Rotated sorted arrays
- Any space with monotonic properties

Core Algorithm Steps

Define boundaries: Initialize left and right pointers to include all possible cases
Define return values: Determine what to return (index, value, -1, etc.)
Define exit condition: Choose appropriate loop condition (<=, <, or < -1)
Update pointers: Move boundaries based on comparison with target

When to Use Binary Search

Sorted arrays: Classic use case for finding exact values
Monotonic functions: If condition(k) implies condition(k+1), binary search applies
Search boundaries: Finding first/last occurrence of a value
Optimization problems: Finding minimum/maximum values satisfying constraints

References

Frameworks:
- labuladong Binary Search Framework
- Binary Search 101 Handbook
Problem Collections:
- Binary Search in Action
- Binary Search Problem Set
Python Tools:
- Python bisect module - maintains sorted order during insertions

1) Binary Search Types & Patterns

1.1) Basic Binary Search

Purpose: Find exact target value in sorted array
Return: Index of target, or -1 if not found
Complexity: O(log n)

1.2) Search in Rotated Array

Key Concept: Determine which half is sorted, then decide search direction
Applications: Find target, find minimum element

Find Minimum in Rotated Sorted Array (LC 153)

// Approach: Compare mid with boundaries to determine rotation point
while (r >= l) {
    int mid = (l + r) / 2;
    // Case 1: left subarray + mid is ascending -> search right
    if (nums[mid] >= nums[l]) {
        l = mid + 1;
    }
    // Case 2: right subarray + mid is ascending -> search left  
    else {
        r = mid - 1;
    }
}

// Two-step approach: determine sorted half, then check target location
while (r >= l) {
    int mid = (l + r) / 2;
    
    if (nums[mid] == target) {
        return mid;
    }
    
    // Case 1: Left half is sorted (compare mid with left boundary)
    if (nums[mid] >= nums[l]) {
        // Check if target is in the sorted left half
        if (target >= nums[l] && target < nums[mid]) {
            r = mid - 1;  // Search left half
        } else {
            l = mid + 1;  // Search right half
        }
    }
    // Case 2: Right half is sorted
    else {
        // Check if target is in the sorted right half  
        if (target <= nums[r] && target > nums[mid]) {
            l = mid + 1;  // Search right half
        } else {
            r = mid - 1;  // Search left half
        }
    }
}

Key Differences:

LC 153 (Find Min): Only needs to determine which side to search
LC 33/81 (Find Target): Must check target location within sorted half

1.3) Recursive Binary Search

Use Cases: When recursive approach is more intuitive
Space: O(log n) due to call stack

1.4) Search in 2D Matrix (LC 74)

Approach 1: Flatten matrix using row = idx / cols, col = idx % cols
Approach 2: Row-by-row binary search
Time: O(log(m×n))

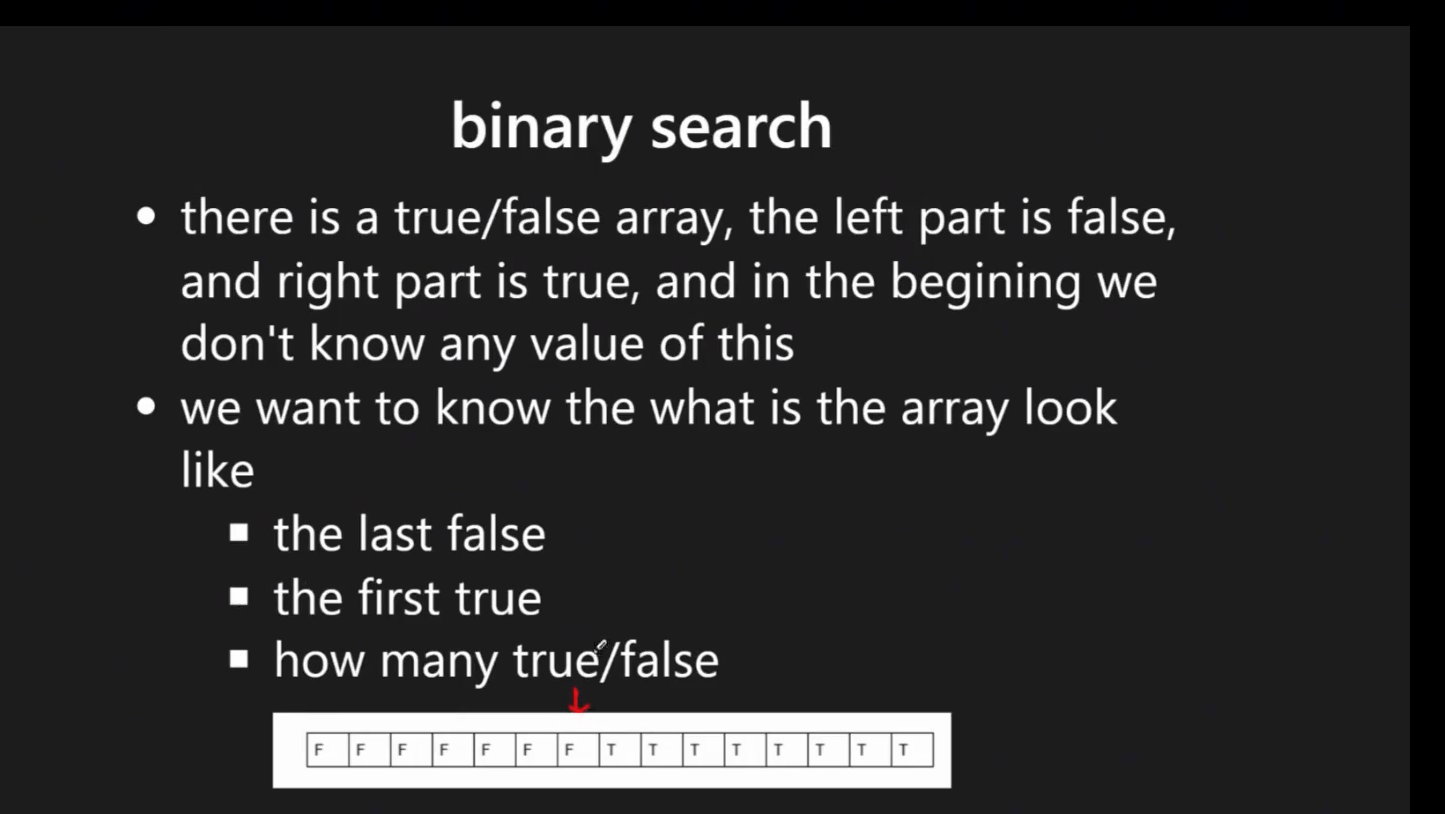
1.5) Find Boundaries (LC 34)

Purpose: Find first and last occurrence of target

// Template for finding boundaries
while (r >= l) {
    int mid = (l + r) / 2;
    
    if (nums[mid] == target) {
        // Key: Don't return immediately, continue searching
        if (findFirst) {
            r = mid - 1;  // Shrink right boundary to find leftmost
        } else {
            l = mid + 1;  // Shrink left boundary to find rightmost  
        }
    } else if (nums[mid] < target) {
        l = mid + 1;
    } else {
        r = mid - 1;
    }
}
// Post-processing needed to validate result

1.6) Left Boundary Search (LC 367, 875)

Purpose: Find the leftmost occurrence of target

def find_left_boundary(nums, target):
    l, r = 0, len(nums) - 1
    
    while l <= r:
        mid = l + (r - l) // 2
        if nums[mid] < target:
            l = mid + 1
        elif nums[mid] > target:
            r = mid - 1
        else:  # nums[mid] == target
            r = mid - 1  # Keep searching left
    
    # Validate result
    if l >= len(nums) or nums[l] != target:
        return -1
    return l

// Generic left boundary template
while (r >= l) {
    int mid = (l + r) / 2;
    if (condition(mid)) {
        r = mid - 1;  // Found valid, search for better (smaller) solution
    } else {
        l = mid + 1;  // Not valid, search larger values
    }
}
// Result is typically at index 'l'

1.7) Right Boundary Search

Purpose: Find the rightmost occurrence of target

def find_right_boundary(nums, target):
    l, r = 0, len(nums) - 1
    
    while l <= r:
        mid = l + (r - l) // 2
        if nums[mid] < target:
            l = mid + 1
        elif nums[mid] > target:
            r = mid - 1
        else:  # nums[mid] == target
            l = mid + 1  # Keep searching right
    
    # Validate result  
    if r < 0 or nums[r] != target:
        return -1
    return r

Complementary Algorithms:

Two Pointers: For sorted arrays without random access
Sliding Window: For subarray problems with certain properties
Recursion: Alternative implementation approach

Data Structures:

Arrays: Primary use case for binary search
Binary Search Trees: Implicit binary search in tree traversal
Hash Tables: O(1) lookup alternative when sorting not required

2) Binary Search Templates & Patterns

Additional Resources

0-2-0) Loop Exit Conditions Comparison

Key Difference: The exit condition determines when the loop terminates and affects boundary handling.

Condition	Boundary Type	When to Use	Key Characteristics
`while (l <= r)`	Closed [l, r]	Standard binary search	• Most common approach • Search space includes both l and r • Need `l = mid + 1`, `r = mid - 1`
`while (l < r)`	Half-open [l, r)	Finding boundaries/insertion points	• Search space excludes r • Loop ends when `l == r` • Use `l = mid + 1`, `r = mid`
`while (l < r - 1)`	Gap-based	Avoiding infinite loops in special cases	• Ensures l and r are never adjacent • Requires final check after loop • Less common, used for complex conditions

Detailed Analysis:

// 1) while (l <= r) - CLOSED BOUNDARY [l, r]
while (l <= r) {
    int mid = l + (r - l) / 2;
    if (nums[mid] == target) return mid;
    else if (nums[mid] < target) l = mid + 1;  // MUST +1
    else r = mid - 1;                          // MUST -1
}
// Pros: Standard, easy to understand
// Cons: Can return -1 if not found

// 2) while (l < r) - HALF-OPEN [l, r)
while (l < r) {
    int mid = l + (r - l) / 2;
    if (nums[mid] < target) l = mid + 1;       // +1 to exclude mid
    else r = mid;                              // NO -1, keep mid in range
}
// After loop: l == r, points to answer or insertion point
// Pros: Great for finding boundaries, no -1 return
// Cons: Requires different logic for different problems

// 3) while (l < r - 1) - GAP-BASED
while (l < r - 1) {
    int mid = l + (r - l) / 2;
    if (condition(mid)) l = mid;
    else r = mid;
}
// Final check needed: examine both l and r
// Pros: Avoids infinite loops in complex conditions
// Cons: More complex, requires post-processing

When to Use Each:

while (l <= r): Classic binary search, finding exact values
while (l < r): Finding first/last occurrence, insertion position, peak finding
while (l < r - 1): Complex conditions where mid might equal l or r

Classic LeetCode Problems by Pattern

Pattern 1: while (l <= r) - Exact Search

LC 704: Binary Search (basic implementation)
LC 33: Search in Rotated Sorted Array
LC 81: Search in Rotated Sorted Array II
LC 74: Search a 2D Matrix
LC 240: Search a 2D Matrix II
LC 69: Sqrt(x)
LC 367: Valid Perfect Square
LC 441: Arranging Coins

Pattern 2: while (l < r) - Boundary/Peak Finding

LC 34: Find First and Last Position of Element
LC 35: Search Insert Position
LC 162: Find Peak Element
LC 852: Peak Index in a Mountain Array
LC 153: Find Minimum in Rotated Sorted Array
LC 154: Find Minimum in Rotated Sorted Array II
LC 278: First Bad Version
LC 658: Find K Closest Elements
LC 744: Find Smallest Letter Greater Than Target

Pattern 3: while (l < r - 1) - Complex Conditions

LC 410: Split Array Largest Sum (with validation function)
LC 875: Koko Eating Bananas (with time calculation)
LC 1011: Capacity To Ship Packages Within D Days
LC 1060: Missing Element in Sorted Array
LC 1482: Minimum Number of Days to Make m Bouquets

2.1) Standard Binary Search Template

Key Principles:

Initialization: left = 0, right = nums.length - 1 (closed interval)
Loop Condition: while (left <= right)
Pointer Updates: left = mid + 1, right = mid - 1
Clarity Tip: Use else if for all conditions to make logic explicit

Programming Tip: Avoid using else - write all conditions as else if to clearly show all cases and avoid bugs.

// Java Implementation
public int binarySearch(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    
    // Use <= to search when left == right
    while (left <= right) {
        int mid = left + (right - left) / 2;  // Avoid overflow
        
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1;   // Target in right half
        } else {  // nums[mid] > target
            right = mid - 1;  // Target in left half
        }
    }
    return -1;  // Not found
}

# Python Implementation  
def binary_search(nums, target):
    left, right = 0, len(nums) - 1
    
    # Closed boundary [left, right] - includes both endpoints
    while left <= right:
        mid = left + (right - left) // 2  # Avoid overflow
        
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid + 1   # Search right half
        else:
            right = mid - 1  # Search left half
            
    return -1  # Target not found

2.2) Left Boundary Template

Use Cases: Find leftmost occurrence, insertion point, first valid solution

/**
 * Key Differences from Standard Binary Search:
 * 1. When nums[mid] == target: shrink RIGHT boundary (right = mid - 1)
 * 2. Post-processing: validate the result before returning
 */
public int findLeftBoundary(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    
    while (left <= right) {
        int mid = left + (right - left) / 2;
        
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else {  // nums[mid] == target
            // DON'T return! Continue searching for leftmost occurrence
            right = mid - 1;  // Shrink right boundary
        }
    }
    
    // Validate result - check bounds and target match
    if (left >= nums.length || nums[left] != target) {
        return -1;
    }
    return left;
}

# Python Left Boundary Implementation
def find_left_boundary(nums, target):
    left, right = 0, len(nums) - 1
    
    while left <= right:
        mid = left + (right - left) // 2
        
        if nums[mid] < target:
            left = mid + 1
        elif nums[mid] > target:
            right = mid - 1
        else:  # nums[mid] == target
            # Continue searching left for first occurrence
            right = mid - 1
    
    # Validate: check if left is within bounds and points to target
    if left >= len(nums) or nums[left] != target:
        return -1
    return left

2.3) Right Boundary Template

Use Cases: Find rightmost occurrence, last valid solution

/**
 * Key Differences from Standard Binary Search:
 * 1. When nums[mid] == target: shrink LEFT boundary (left = mid + 1)
 * 2. Return left - 1 after validation
 */
public int findRightBoundary(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    
    while (left <= right) {
        int mid = left + (right - left) / 2;
        
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else {  // nums[mid] == target
            // DON'T return! Continue searching for rightmost occurrence
            left = mid + 1;  // Shrink left boundary
        }
    }
    
    // Validate result - return left - 1
    if (right < 0 || nums[right] != target) {
        return -1;
    }
    return right;
}

# Python Right Boundary Implementation
def find_right_boundary(nums, target):
    left, right = 0, len(nums) - 1
    
    while left <= right:
        mid = left + (right - left) // 2
        
        if nums[mid] < target:
            left = mid + 1
        elif nums[mid] > target:
            right = mid - 1
        else:  # nums[mid] == target
            # Continue searching right for last occurrence
            left = mid + 1
    
    # Validate: check if right is within bounds and points to target
    if right < 0 or nums[right] != target:
        return -1
    return right

3) Summary & Quick Reference

3.1) When to Use Binary Search

✅ Use Binary Search When:

Array is sorted (fully, partially, or rotationally)
Search space has monotonic property
Need O(log n) search performance
Looking for boundaries or insertion points
Optimization problems with binary nature

3.2) Template Selection Guide

Problem Type	Template	Key Characteristics
Exact Search	Standard (`while l <= r`)	Return index or -1
Left Boundary	Left Template	Find first occurrence
Right Boundary	Right Template	Find last occurrence
Insert Position	Left Template	Find insertion point
Peak/Valley	Half-open (`while l < r`)	Converge to answer
Complex Conditions	Gap-based (`while l < r-1`)	Avoid infinite loops

3.3) Common Pitfalls & Tips

🚫 Common Mistakes:

Integer overflow in mid = (left + right) / 2 → Use mid = left + (right - left) / 2
Wrong boundary updates (mid vs mid ± 1)
Forgetting post-processing validation
Infinite loops with while l < r and wrong updates

✅ Best Practices:

Always use else if for clarity
Validate results after boundary searches
Choose consistent boundary type (closed vs half-open)
Test with edge cases: empty array, single element, duplicates

3.4) Time & Space Complexity

Time: O(log n) for search, O(n) for validation if needed
Space: O(1) iterative, O(log n) recursive

4) LeetCode Examples & Applications

This section demonstrates how to apply binary search patterns to solve specific problems.

4.1) Search in Rotated Sorted Array (LC 33, LC 81)

# LC 033. Search in Rotated Sorted Array
# LC 081. Search in Rotated Sorted Array II
# V0
# IDEA : BINARY SEARCH
#        -> CHECK WHICH PART IS ORDERING
#        -> CHECK IF TARGET IS IN WHICH PART
# CASES :
#  1) if mid is on the right of pivot -> array[mid:] is ordering
#     -> check if mid in on the left or right on mid
#     -> binary search on left or right sub array
#  2) if mid in on the left of pivot  -> array[:mid] is ordering
#     -> check if mid in on the left or right on mid
#     -> binary search on left or right sub array
### NOTE : THE NESTED IF ELSE CONDITION 
class Solution(object):
    def search(self, nums, target):
        if not nums: return -1
        left, right = 0, len(nums) - 1
        while left <= right:
            mid = (left + right) // 2
            if nums[mid] == target:
                return mid
            #---------------------------------------------
            # Case 1 :  nums[mid:right] is ordering
            #---------------------------------------------
            # all we need to do is : 1) check if target is within mid - right, and move the left or right pointer
            if nums[mid] < nums[right]:
                # mind NOT use (" nums[mid] < target <= nums[right]")
                # mind the "<="
                if target > nums[mid] and target <= nums[right]: # check the relationship with target, which is different from the default binary search
                    left = mid + 1
                else:
                    right = mid - 1
            #---------------------------------------------
            # Case 2 :  nums[left:mid] is ordering
            #---------------------------------------------
            # all we need to do is : 1) check if target is within left - mid, and move the left or right pointer
            else:
                # # mind NOT use (" nums[left] <= target < nums[mid]")
                # mind the "<="
                if target < nums[mid] and target >= nums[left]:  # check the relationship with target, which is different from the default binary search
                    right = mid - 1
                else:
                    left = mid + 1
        return -1     

// java
// LC 33
// V3
// IDEA : One Binary Search
// https://leetcode.com/problems/search-in-rotated-sorted-array/editorial/
public int search_4(int[] nums, int target) {
    int n = nums.length;
    int left = 0, right = n - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        // Case 1: find target
        if (nums[mid] == target) {
            return mid;
        }

        // Case 2: subarray on mid's left is sorted
        else if (nums[mid] >= nums[left]) {
            if (target >= nums[left] && target < nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        // Case 3: subarray on mid's right is sorted
        else {
            if (target <= nums[right] && target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
    }

    return -1;
}

4.2) Two Sum II - Input Array is Sorted (LC 167)

Approach: Binary search for each element’s complement

# 167 Two Sum II - Input array is sorted
class Solution(object):
    def twoSum(self, numbers, target):
        for i in range(len(numbers)):
            l, r = i+1, len(numbers)-1
            tmp = target - numbers[i]
            while l <= r:
                mid = l + (r-l)//2
                if numbers[mid] == tmp:
                    return [i+1, mid+1]
                elif numbers[mid] < tmp:
                    l = mid+1
                else:
                    r = mid-1

4.3) Find Peak Element (LC 162, LC 852)

Approach: Compare mid with adjacent elements to determine search direction

# LC 162 Find Peak Element, LC 852 Peak Index in a Mountain Array
# V0'
# IDEA : RECURSIVE BINARY SEARCH
class Solution(object):
    def findPeakElement(self, nums):

        def help(nums, l, r):
            if l == r:
                return l
            mid = l + (r - l) // 2
            if (nums[mid] > nums[mid+1]):
                return help(nums, l, mid) # r = mid
            return help(nums, mid+1, r) # l = mid + 1
            
        return help(nums, 0, len(nums)-1)

// java
// LC 162
// V2
// IDEA: RECURSIVE BINARY SEARCH
// https://leetcode.com/problems/find-peak-element/editorial/
    // NOTE : ONLY have to compare index i with index i + 1 (its right element)
    //        ; otherwise, i-1 already returned as answer
    public int findPeakElement_2(int[] nums) {
        return search(nums, 0, nums.length - 1);
    }
    public int search(int[] nums, int l, int r) {
        if (l == r)
            return l;
        int mid = (l + r) / 2;
        if (nums[mid] > nums[mid + 1])
            return search(nums, l, mid);
        return search(nums, mid + 1, r);
    }

// V3
// IDEA: ITERATIVE BINARY SEARCH
// https://leetcode.com/problems/find-peak-element/editorial/
    public int findPeakElement_3(int[] nums) {
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int mid = (l + r) / 2;
            if (nums[mid] > nums[mid + 1])
                r = mid;
            else
                l = mid + 1;
        }
        return l;
    }

4.4) Valid Perfect Square (LC 367) & Sqrt(x) (LC 69)

Approach: Binary search on the range [1, num] to find square root

# 367 Valid Perfect Square, LC 69 Sqrt(x)
# V0'
# IDEA : BINARY SEARCH
class Solution(object):
    def isPerfectSquare(self, num):
        left, right = 0, num
        while left <= right:
            ### NOTE : there is NO mid * mid == num condition
            mid = (left + right) / 2
            if mid * mid >= num:
                right = mid - 1
            else:
                left = mid + 1
        ### NOTE this
        return left * left == num

// java
// LC 367
public boolean isPerfectSquare(int num) {

    if (num < 2) {
        return true;
    }

    long left = 2;
    long right = num / 2; // NOTE !!!, "long right = num;" is OK as well
    long x;
    long guessSquared;

    while (left <= right) {
        x = (left + right) / 2;
        guessSquared = x * x;
        if (guessSquared == num) {
            return true;
        }
        if (guessSquared > num) {
            right = x - 1;
        } else {
            left = x + 1;
        }
    }
    return false;
}

4.5) Minimum Size Subarray Sum (LC 209)

Approach: Binary search on possible subarray lengths + sliding window validation

# LC 209 Minimum Size Subarray Sum
### NOTE : there is also sliding window approach
# V1' 
# http://bookshadow.com/weblog/2015/05/12/leetcode-minimum-size-subarray-sum/
# IDEA : BINARY SEARCH 
class Solution:
    def minSubArrayLen(self, s, nums):
        size = len(nums)
        left, right = 0, size
        bestAns = 0
        while left <= right:
            mid = (left + right) / 2
            if self.solve(mid, s, nums):
                bestAns = mid
                right = mid - 1
            else:
                left = mid + 1
        return bestAns

    def solve(self, l, s, nums):
        sums = 0
        for x in range(len(nums)):
            sums += nums[x]
            if x >= l:
                sums -= nums[x - l]
            if sums >= s:
                return True
        return False

4.6) First Bad Version (LC 278)

Approach: Binary search to find the first occurrence where isBadVersion() returns true

# LC 278
# V0
# IDEA : binary search
class Solution(object):
    def firstBadVersion(self, n):
        left = 1 
        right = n
        while right > left + 1:
            mid = (left + right)//2
            if SVNRepo.isBadVersion(mid):
                end = mid 
            else:
                left = mid 
        if SVNRepo.isBadVersion(left):
            return left
        return right 

4.7) Search Insert Position (LC 35)

Approach: Find leftmost position where target can be inserted

# LC 035 Search Insert Position
# V1' 
# https://blog.csdn.net/fuxuemingzhu/article/details/70738108
class Solution(object):
    def searchInsert(self, nums, target):
        N = len(nums)
        left, right = 0, N #[left, right)
        while left < right:
            mid = left + (right - left) / 2
            if nums[mid] == target:
                return mid
            elif nums[mid] > target:
                right = mid
            else:
                left = mid + 1
        return left

4.8) Capacity To Ship Packages Within D Days (LC 1011)

Approach: Binary search on capacity + greedy validation

# LC 1011
# V1
# IDEA : BINARY SEARCH
# https://leetcode.com/problems/capacity-to-ship-packages-within-d-days/discuss/390359/Simple-Python-Binary-Search
# V0
# IDEA : BINARY SEARCH
class Solution(object):
     def shipWithinDays(self, weights, D):
            """
            NOTE !!!
                -> for this help func,
                -> we ONLY need to check weights can split by offered max_wgt
                -> so the return val is boolean (True or False)
            """
            # help func
            def cannot_split(weights, D, max_wgt):
                s = 0
                days = 1
                for w in weights:
                    s += w
                    if s > max_wgt:
                        s = w
                        days += 1
                return days > D

            """
            NOTE this !!!
                -> for l, we use max(weights)
                -> for r, we use sum(weights)
            """
            l = max(weights)
            r = sum(weights)
            while l <= r:
                mid = l + (r - l) // 2
                if cannot_split(weights, D, mid):
                    l = mid + 1
                else:
                    r = mid - 1
            return l

4.9) Split Array Largest Sum (LC 410) [Hard]

Approach: Binary search on the maximum sum + greedy partitioning

# LC 410 Split Array Largest Sum [Hard]

4.10) Koko Eating Bananas (LC 875)

Approach: Binary search on eating speed + time calculation validation

// java
// LC 875

// V0
// IDEA : BINARY SEARCH (close boundary)
/**
 *  KEY !!!!
 *
 *   -> When r < l, it means the `smallest` valid eating speed is l
 *
 */
public int minEatingSpeed(int[] piles, int h) {

    if (piles.length == 0 || piles.equals(null)){
        return 0;
    }

    int l = 1; //Arrays.stream(piles).min().getAsInt();
    int r = Arrays.stream(piles).max().getAsInt();

    while (r >= l){
        int mid = (l + r) / 2;
        int _hour = getCompleteTime(piles, mid);
        if (_hour <= h){
            r = mid - 1;
        }else{
            l = mid + 1;
        }
    }

    return l;
}

4.11) Find K Closest Elements (LC 658)

Approach: Two pointers approach to shrink array to k elements

# LC 658. Find K Closest Elements
# V1'
# https://blog.csdn.net/fuxuemingzhu/article/details/82968136
# IDEA : TWO POINTERS 
class Solution(object):
    def findClosestElements(self, arr, k, x):
        # since the array already sorted, arr[-1] must be the biggest one,
        # while arr[0] is the smallest one
        # so if the distance within arr[-1],  x >  arr[0],  x
        # then remove the arr[-1] since we want to keep k elements with smaller distance,
        # and vice versa (remove arr[0]) 
        while len(arr) > k:
            if x - arr[0] <= arr[-1] - x:
                arr.pop()
            else:
                arr.pop(0)
        return arr

4.12) Sqrt(x) (LC 69) - Alternative Implementation

Approach: Binary search with careful boundary handling

# LC 069 Sqrt(x)
# V0
# IDEA : binary search
class Solution(object):
    def mySqrt(self, x):
        # edge case
        if not x or x <= 0:
            return 0
        if x == 1:
            return 1
        l = 0
        r = x-1
        while r >= l:
            mid = l + (r-l)//2
            #print ("l = " + str(l) + " r = " + str(r) + " mid = " + str(mid))
            sq = mid** 2
            if sq == x:
                return mid
            elif sq < x:
                if (mid+1)**2 > x:
                    return mid
                l = mid + 1
            else:
                r = mid - 1

# V0
# IDEA : binary search
class Solution(object):
    def mySqrt(self, num):
        if num <= 1:
            return num
        l = 0
        r = num - 1
        while r >= l:
            mid = l + (r - l) // 2
            if mid * mid == num:
                return mid
            elif mid * mid > num:
                r = mid - 1
            else:
                l = mid + 1
        return l if l * l < num else l - 1

4.13) Find First and Last Position of Element in Sorted Array (LC 34)

Approach: Use left and right boundary search templates

# 34. Find First and Last Position of Element in Sorted Array
# V0
# IDEA : BINARY SEARCH
class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        
        def search(x):
            lo, hi = 0, len(nums)           
            while lo < hi:
                mid = (lo + hi) // 2
                if nums[mid] < x:
                    lo = mid+1
                else:
                    hi = mid                    
            return lo
        
        lo = search(target)
        hi = search(target+1)-1
        
        if lo <= hi:
            return [lo, hi]
                
        return [-1, -1]

// java
// LC 34

// V0
// IDEA: BINARY SEARCH (fixed by gpt)
public int[] searchRange(int[] nums, int target) {
    int[] res = new int[]{-1, -1}; // Default result

    if (nums == null || nums.length == 0) {
        return res;
    }

    // Find the first occurrence of target
    int left = findBound(nums, target, true);
    if (left == -1) {
        return res; // Target not found
    }

    // Find the last occurrence of target
    int right = findBound(nums, target, false);

    return new int[]{left, right};
}

private int findBound(int[] nums, int target, boolean isFirst) {
    int l = 0, r = nums.length - 1;
    int bound = -1;

    while (l <= r) {
        int mid = l + (r - l) / 2;

        if (nums[mid] == target) {
            bound = mid;
            if (isFirst) {
                r = mid - 1; // Keep searching left
            } else {
                l = mid + 1; // Keep searching right
            }
        } else if (nums[mid] < target) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }

    return bound;
}

4.14) Search a 2D Matrix (LC 74)

Approach: Flatten 2D matrix to 1D using index conversion

// java
// LC 74
// V1
// IDEA : BINARY SEARCH + FLATTEN MATRIX
// https://leetcode.com/problems/search-a-2d-matrix/editorial/
public boolean searchMatrix_2(int[][] matrix, int target) {
    int m = matrix.length;
    if (m == 0)
        return false;
    int n = matrix[0].length;

    // binary search
    /** NOTE !!! FLATTEN MATRIX */
    int left = 0, right = m * n - 1;
    int pivotIdx, pivotElement;
    while (left <= right) {
        pivotIdx = (left + right) / 2;
        /** NOTE !!! TRICK HERE :
         *
         *   pivotIdx / n : y index
         *   pivotIdx % n : x index
         */
        pivotElement = matrix[pivotIdx / n][pivotIdx % n];
        if (target == pivotElement)
            return true;
        else {
            if (target < pivotElement)
                right = pivotIdx - 1;
            else
                left = pivotIdx + 1;
        }
    }
    return false;
}

4.15) Find Minimum in Rotated Sorted Array (LC 153)

Approach: Compare mid with boundaries to find rotation point

// java
// LC 153

    // V0
    // IDEA : BINARY SEARCH (CLOSED BOUNDARY)
    // https://youtu.be/nIVW4P8b1VA?si=AMhTJOUhDziBz-CV
    /**
     *  NOTE !!!
     *
     *  key : check current `mid point` is at  `left part` or `right part`
     *  if `at left part`
     *   -> nums[l] ~ nums[mid] is in INCREASING order
     *   -> need to search `RIGHT part`, since right part is ALWAYS SMALLER then left part
     *
     *  else, `at right part`
     *   -> need to search `LEFT part`
     */
    public int findMin(int[] nums) {
        int l = 0;
        int r = nums.length - 1;
        int res = nums[0];

        /** NOTE !!! closed boundary */
        while (l <= r) {

            // edge case : is array already in increasing order (e.g. [1,2,3,4,5])
            if (nums[l] < nums[r]) {
                res = Math.min(res, nums[l]);
                break;
            }

            int m = l + (r - l) / 2;
            res = Math.min(res, nums[m]);

            // case 1) mid point is at `LEFT part`
            // e.g. [3,4,5,1,2]
            if (nums[m] >= nums[l]) {
                l = m + 1;
            }
            // case 2) mid point is at `RIGHT part`
            // e.g. [5,1,2,3,4]
            else {
                r = m - 1;
            }
        }
        return res;
    }

4.16) Find First and Last Position - Alternative Implementation

Approach: Separate functions for finding first and last occurrences

// java
// LC 34
    public int[] searchRange_1(int[] nums, int target) {
        int[] result = new int[2];
        result[0] = findFirst(nums, target);
        result[1] = findLast(nums, target);
        return result;
    }

    private int findFirst(int[] nums, int target) {
        int idx = -1;
        int start = 0;
        int end = nums.length - 1;
        while (start <= end) {
            int mid = (start + end) / 2;

            /** NOTE !!!
             *
             * 1) nums[mid] >= target (find right boundary)
             * 2) we put equals condition below  (nums[mid] == target)
             */
            if (nums[mid] >= target) {
                end = mid - 1;
            } else {
                start = mid + 1;
            }
            if (nums[mid] == target)
                idx = mid;
        }
        return idx;
    }

    private int findLast(int[] nums, int target) {
        int idx = -1;
        int start = 0;
        int end = nums.length - 1;
        while (start <= end) {
            int mid = (start + end) / 2;
            /** NOTE !!!
             *
             * 1) nums[mid] <= target (find left boundary)
             * 2) we put equals condition below  (nums[mid] == target)
             */
            if (nums[mid] <= target) {
                start = mid + 1;
            } else {
                end = mid - 1;
            }
            if (nums[mid] == target)
                idx = mid;
        }
        return idx;
    }

4.17) Find Smallest Letter Greater Than Target (LC 744)

Pattern: while (l < r) - Finding insertion position

# LC 744 Find Smallest Letter Greater Than Target
class Solution(object):
    def nextGreatestLetter(self, letters, target):
        l, r = 0, len(letters)
        
        # Use half-open boundary [l, r)
        while l < r:
            mid = l + (r - l) // 2
            if letters[mid] <= target:  # Need strictly greater
                l = mid + 1
            else:
                r = mid
        
        # Handle circular array - if no letter greater than target, return first
        return letters[l % len(letters)]

4.18) Arranging Coins (LC 441)

Pattern: while (l <= r) - Finding exact value with mathematical property

// LC 441 Arranging Coins
public int arrangeCoins(int n) {
    long l = 0, r = n;
    
    while (l <= r) {
        long mid = l + (r - l) / 2;
        long coins = mid * (mid + 1) / 2;  // Sum of 1+2+...+mid
        
        if (coins == n) {
            return (int) mid;
        } else if (coins < n) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    
    return (int) r;  // Return the complete rows we can form
}

4.19) Minimum Number of Days to Make m Bouquets (LC 1482)

Pattern: while (l < r - 1) - Complex validation with helper function

# LC 1482 Minimum Number of Days to Make m Bouquets
class Solution(object):
    def minDays(self, bloomDay, m, k):
        if m * k > len(bloomDay):
            return -1
        
        def canMakeBouquets(days):
            bouquets = consecutive = 0
            for bloom in bloomDay:
                if bloom <= days:
                    consecutive += 1
                    if consecutive == k:
                        bouquets += 1
                        consecutive = 0
                else:
                    consecutive = 0
            return bouquets >= m
        
        l, r = min(bloomDay), max(bloomDay)
        
        while l < r:
            mid = l + (r - l) // 2
            if canMakeBouquets(mid):
                r = mid
            else:
                l = mid + 1
        
        return l

4.20) Search a 2D Matrix II (LC 240)

Pattern: while (l <= r) - Search with elimination technique

# LC 240 Search a 2D Matrix II
class Solution(object):
    def searchMatrix(self, matrix, target):
        if not matrix or not matrix[0]:
            return False
        
        # Start from top-right corner
        row, col = 0, len(matrix[0]) - 1
        
        while row < len(matrix) and col >= 0:
            if matrix[row][col] == target:
                return True
            elif matrix[row][col] > target:
                col -= 1  # Move left
            else:
                row += 1  # Move down
        
        return False

4.21) Find Minimum in Rotated Sorted Array II (LC 154)

Pattern: while (l < r) - Handling duplicates in rotated array

// LC 154 Find Minimum in Rotated Sorted Array II (with duplicates)
public int findMin(int[] nums) {
    int l = 0, r = nums.length - 1;
    
    while (l < r) {
        int mid = l + (r - l) / 2;
        
        if (nums[mid] < nums[r]) {
            // Right half is sorted, minimum is in left half (including mid)
            r = mid;
        } else if (nums[mid] > nums[r]) {
            // Left half is sorted, minimum is in right half
            l = mid + 1;
        } else {
            // nums[mid] == nums[r], can't determine which half to search
            // Reduce search space by 1
            r--;
        }
    }
    
    return nums[l];
}

4.22) Missing Element in Sorted Array (LC 1060)

Pattern: while (l < r - 1) - Finding missing elements with gap calculation

# LC 1060 Missing Element in Sorted Array
class Solution(object):
    def missingElement(self, nums, k):
        def missing_count(idx):
            # How many numbers are missing up to nums[idx]
            return nums[idx] - nums[0] - idx
        
        n = len(nums)
        
        # If k-th missing number is beyond the array
        if k > missing_count(n - 1):
            return nums[-1] + k - missing_count(n - 1)
        
        l, r = 0, n - 1
        
        # Find the largest index where missing_count < k
        while l < r - 1:
            mid = l + (r - l) // 2
            if missing_count(mid) < k:
                l = mid
            else:
                r = mid
        
        # The k-th missing number is between nums[l] and nums[r]
        return nums[l] + k - missing_count(l)

Binary Search

Overview

Key Properties

Core Algorithm Steps

When to Use Binary Search

References

1) Binary Search Types & Patterns

1.1) Basic Binary Search

1.2) Search in Rotated Array

Find Minimum in Rotated Sorted Array (LC 153)

1.3) Recursive Binary Search

1.4) Search in 2D Matrix (LC 74)

1.5) Find Boundaries (LC 34)

1.6) Left Boundary Search (LC 367, 875)

1.7) Right Boundary Search

1.8) Related Algorithms & Data Structures

2) Binary Search Templates & Patterns

Additional Resources

0-2-0) Loop Exit Conditions Comparison

Classic LeetCode Problems by Pattern

2.1) Standard Binary Search Template

2.2) Left Boundary Template

2.3) Right Boundary Template

3) Summary & Quick Reference

3.1) When to Use Binary Search

3.2) Template Selection Guide

3.3) Common Pitfalls & Tips

3.4) Time & Space Complexity

4) LeetCode Examples & Applications

4.1) Search in Rotated Sorted Array (LC 33, LC 81)

4.2) Two Sum II - Input Array is Sorted (LC 167)

4.3) Find Peak Element (LC 162, LC 852)

4.4) Valid Perfect Square (LC 367) & Sqrt(x) (LC 69)

4.5) Minimum Size Subarray Sum (LC 209)

4.6) First Bad Version (LC 278)

4.7) Search Insert Position (LC 35)

4.8) Capacity To Ship Packages Within D Days (LC 1011)

4.9) Split Array Largest Sum (LC 410) [Hard]

4.10) Koko Eating Bananas (LC 875)

4.11) Find K Closest Elements (LC 658)

4.12) Sqrt(x) (LC 69) - Alternative Implementation

4.13) Find First and Last Position of Element in Sorted Array (LC 34)

4.14) Search a 2D Matrix (LC 74)

4.15) Find Minimum in Rotated Sorted Array (LC 153)

4.16) Find First and Last Position - Alternative Implementation

4.17) Find Smallest Letter Greater Than Target (LC 744)

4.18) Arranging Coins (LC 441)

4.19) Minimum Number of Days to Make m Bouquets (LC 1482)

4.20) Search a 2D Matrix II (LC 240)

4.21) Find Minimum in Rotated Sorted Array II (LC 154)

4.22) Missing Element in Sorted Array (LC 1060)